Có bao nhiêu giá trị nguyên của tham số \(m\) để đường thẳng \(y = m\left( {x - 4} \right)\) cắt đồ thị của hàm số \(y = \left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)\) tại bốn điểm phân biệt?
Phương pháp giải
- Xét phương trình hoành độ giao điểm của hai đồ thị hàm số.
- Cô lập \(m\) đưa phương trình về dạng \(f\left( x \right) = g\left( m \right)\)
- Xét hàm số \(y = f\left( x \right)\), lập bảng biến thiên và kết luận, chú ý số giao điểm của hai đồ thị hàm số là số nghiệm của phương trình hoành độ giao điểm.
Lời giải của Tự Học 365
Ta có phương trình hoành độ giao điểm
\(\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right) = m\left( {x - 4} \right)\) \( \Rightarrow \,\,\,\,\,\dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}} = m\,\,\,\,\left( 1 \right)\), \(\left( {x e 4} \right)\)
Số nghiệm của \(\left( 1 \right)\) bằng số giao điểm của 2 đồ thị hàm số \(y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}}\) và \(y = m\)
Ta có: \(f'\left( x \right) = \dfrac{{2x\left( {{x^2} - 9} \right)\left( {x - 4} \right) + 2x\left( {{x^2} - 1} \right)\left( {x - 4} \right) - \left( {{x^2} - 9} \right)\left( {{x^2} - 1} \right)}}{{{{\left( {x - 4} \right)}^2}}} = \dfrac{{3{x^4} - 16{x^3} - 10{x^2} + 80x - 9}}{{{{\left( {x - 4} \right)}^2}}}\)
\(f'\left( x \right) = 0\,\,\,\,\, \Rightarrow \,\,\,\,\,3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0\)
Giải phương trình bằng MTBT:
- Mở chức năng Table (MODE 7)
Nhập vào máy tính hàm: \(f\left( x \right) = 3{x^4} - 16{x^3} - 10{x^2} + 80x - 9\)
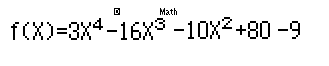
Ấn \('' = ''\) rồi đến bước Start ấn \('' - 7''\), bước End ấn \(''7''\), bước Step ấn \(''1''\) rồi ấn \('' = ''\)
Quan sát bảng và tìm các giá trị của \(x\) mà \(f\left( x \right)\) đột ngột chuyển từ âm sang dương và dương sang âm, ở đây là \( - 3; - 2;0;1;3;5\)
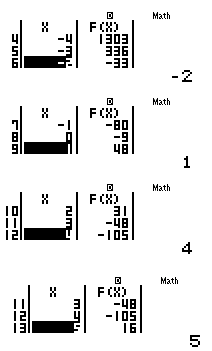
- Thoát ra ngoài (MODE 1) và nhập: \(3{x^4} - 16{x^3} - 10{x^2} + 80x - 9 = 0\)
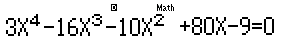
Sử dụng chức năng giải phương trình
+ Ấn SHIFT + SOLVE, nhập \( - 3\) ta được một nghiệm \({x_1} = - 2,1685...\)
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập \( - 2\) ta được một nghiệm \({x_1} = - 2,1685...\)
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập \(0\) ta được một nghiệm \({x_2} = 0,114...\)
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập \(1\) ta được một nghiệm \({x_2} = 0,114...\)
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SLOVE, nhập \(3\) ta được một nghiệm \({x_3} = 2,447...\)
+ Ấn phím mũi tên trái để quay về phương trình vừa nhập.
+ Ấn SHIFT + SOLVE, nhập \(5\) ta được một nghiệm \({x_4} = 4,94...\)
Vậy ta được $4$ nghiệm \(\left[ {\begin{array}{*{20}{c}}{{x_1} \approx - 2,169}\\{{x_2} \approx 0,114}\\{{x_3} \approx 2,45}\\{{x_4} \approx 4,94}\end{array}} \right.\)
Các nghiệm này đã được lưu chính xác ở trong bộ nhớ của MTBT.
Bảng biến thiên:
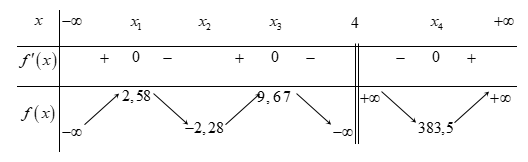
Phương trình đã cho có \(4\) nghiệm phân biệt \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right) = \dfrac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 9} \right)}}{{\left( {x - 4} \right)}}\) tại \(4\) điểm phân biệt
\( \Leftrightarrow m \in \left( { - 2,28;2,58} \right)\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;\,\,0;\,1;\,2} \right\}.\)
Vậy có \(5\) giá trị của \(m\) thỏa bài toán.
Đáp án cần chọn là: b
Toán Lớp 12
