Cho hình thoi \(ABCD\) có \(AC = 2a\) và \(BD = a.\) Tính \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|\).
Phương pháp giải
- Tìm véc tơ tổng của hai véc tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) bằng cách đưa về các véc tơ \(\overrightarrow {OC} ,\overrightarrow {OD} \).
- Tính độ dài các véc tơ này và kết luận.
Lời giải của Tự Học 365
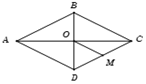
Gọi \(O = AC \cap BD\) và \(M\) là trung điểm của \(CD\).
Ta có \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right| = 2\left| {\overrightarrow {OC} + \overrightarrow {OD} } \right| = 2\left| {2\overrightarrow {OM} } \right| = 4OM\)
\( = 4.\dfrac{1}{2}CD = 2\sqrt {O{D^2} + O{C^2}} = 2\sqrt {\dfrac{{{a^2}}}{4} + {a^2}} = a\sqrt 5 .\)
Đáp án cần chọn là: c
Toán Lớp 12
