Cho tam giác đều\(ABC\) cạnh \(a\), trọng tâm là \(G\). Phát biểu nào là đúng?
Phương pháp giải
- Dựng hình bình hành \(ABDC\).
- Sử dụng các định nghĩa hai véc tơ bằng nhau, quy tắc hình bình hành, tính chất trọng tâm,... để xét tính đúng sai của mỗi đáp án.
Lời giải của Tự Học 365
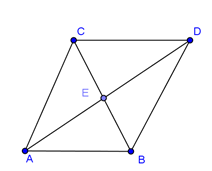
Dựng hình bình hành \(ABDC\) tâm \(E\). Ta có\(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = 2AE = a\sqrt 3 \)
$\sqrt 3 \left| {\overrightarrow {AB} + \overrightarrow {CA} } \right| = \sqrt 3 \left| {\overrightarrow {CB} } \right| = \sqrt 3 CB = \sqrt 3 a$
Vậy $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \sqrt 3 \left| {\overrightarrow {AB} + \overrightarrow {CA} } \right|$.
Đáp án cần chọn là: d
Toán Lớp 12
