Câu hỏi
Vận dụng
Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :
Đáp án đúng: d
Phương pháp giải
- Dựng hình bình hành \(OBFC\) .
- Sử dụng quy tắc hình bình hành tìm véc tơ tổng \(\overrightarrow {OB} + \overrightarrow {OC} \).
- Tính độ dài véc tơ trên sử dụng tính chất hình bình hành và đường trung bình hình thang.
Lời giải của Tự Học 365
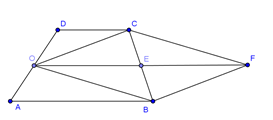
Dựng hình bình hành \(OBFC\) tâm \(E\). Khi đó
$\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = \left| {\overrightarrow {OF} } \right| = OF = 2OE = AB + CD = 3a$.
Đáp án cần chọn là: d
Toán Lớp 12
