Gọi \(G\) là trọng tâm tam giác vuông$ABC$với cạnh huyền $BC = 12$. Tổng hai vectơ $\overrightarrow {GB} + \overrightarrow {GC} $ có độ dài bằng bao nhiêu ?
Phương pháp giải
- Dựng hình bình hành \(GBDC\), sử dụng quy tắc hình bình hành tìm véc tơ tổng \(\overrightarrow {GB} + \overrightarrow {GC} \).
- Tính độ dài véc tơ tìm được ở trên và suy ra kết luận.
Lời giải của Tự Học 365
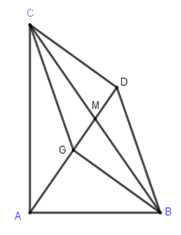
Dựng hình bình hành \(GBDC\). Gọi \(M\) là trung điểm \(BC\).
Tam giác \(ABC\) có trung tuyến \(AM\) nên \(AM = \dfrac{1}{2}BC = \dfrac{1}{2}.12 = 6\)
\( \Rightarrow GM = \dfrac{1}{3}AM = \dfrac{1}{3}.6 = 2\) \( \Rightarrow GD = 2GM = 2.2 = 4\)
Vậy \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right| = GD = 4\)
Đáp án cần chọn là: b
Toán Lớp 12
