Lời giải của Tự Học 365

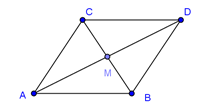
Dựng hình bình hành \(ABDC\) và gọi \(M\) là trung điểm của \(BC\).

Ta có: $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = 2AM$

Trong tam giác đều \(ABC\) có \(AM\) là trung tuyến cũng là đường cao nên \(AM \bot BC,MB = MC = \dfrac{a}{2}\)

Ta có:

\(A{M^2} + M{B^2} = A{B^2}\) \( \Leftrightarrow A{M^2} + {\left( {\dfrac{a}{2}} \right)^2} = {a^2}\) \( \Leftrightarrow A{M^2} = {a^2} - \dfrac{{{a^2}}}{4}\) \( \Leftrightarrow A{M^2} = \dfrac{{3{a^2}}}{4}\) \( \Leftrightarrow AM = \dfrac{{a\sqrt 3 }}{2}\)

Vậy \(AD = 2AM = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \)

Đáp án cần chọn là: a