Lời giải của Tự Học 365

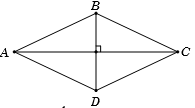
Gọi \(O = AC \cap BD\), giả thiết không cho góc, ta phân tích các vectơ \(\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \) theo các vectơ có giá vuông góc với nhau.Ta có \(\overrightarrow {AB} .\overrightarrow {AC}  = \left( {\overrightarrow {AO}  + \overrightarrow {OB} } \right).\overrightarrow {AC}  = \overrightarrow {AO} .\overrightarrow {AC}  + \overrightarrow {OB} .\overrightarrow {AC} \)\( = \dfrac{1}{2}\overrightarrow {AC} .\overrightarrow {AC}  + 0 = \dfrac{1}{2}A{C^2} = 32\)

Đáp án cần chọn là: d