Câu hỏi
Thông hiểu
Cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(E\) là điểm đối xứng của \(D\) qua \(C.\) Tính \(\overrightarrow {AE} .\overrightarrow {AB} .\)
Đáp án đúng: a
Phương pháp giải
Xen điểm thích hợp và tính tích vô hướng của các véc tơ.
Lời giải của Tự Học 365
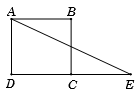
Ta có \(C\) là trung điểm của \(DE\) nên \(DE = 2a.\)
Khi đó \(\overrightarrow {AE} .\overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right).\overrightarrow {AB} = \underbrace {\overrightarrow {AD} .\overrightarrow {AB} }_0 + \overrightarrow {DE} .\overrightarrow {AB} \)
\( = DE.AB.\cos \left( {\overrightarrow {DE} ,\overrightarrow {AB} } \right) = DE.AB.\cos {0^0} = 2{a^2}.\)
Đáp án cần chọn là: a
Toán Lớp 12
