Lời giải của Tự Học 365

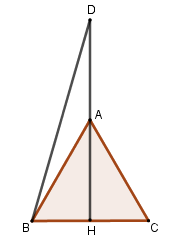
Đáp án A: đúng do \(AH \bot BC\).

Đáp án B: đúng do \(\left( {\overrightarrow {AB} ,\overrightarrow {AH} } \right) = {30^0}\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}.\)

Đáp án C: đúng do \(\overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\) \( = a.a.\cos {60^0} = \dfrac{{{a^2}}}{2}\).

Đáp án D: Do \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\) là góc ngoài của góc \(\widehat A\) nên \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {120^0}.\)

Do đó \(\overrightarrow {AC} .\overrightarrow {CB}  = AC.CB.cos\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\)\( = a.a.cos{120^0} =  - \dfrac{{{a^2}}}{2}\)

Đáp án cần chọn là: d