Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC,\,\,\,G\) là trọng tâm của tam giác\(ABC.\) Khẳng định nào sau đây đúng ?
Phương pháp giải
Sử dụng phương pháp biểu diễn một véc tơ qua hai véc tơ không cùng phương.
Xen điểm và sử dụng mỗi quan hệ giữa các véc tơ.
Lời giải của Tự Học 365
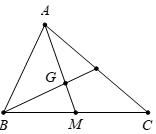
Vì \(G\) là trọng tâm của tam giác \(ABC\)\( \Rightarrow \overrightarrow {AG} = \dfrac{2}{3}\overrightarrow {AM} .\)
Và \(M\) là trung điểm của \(BC\)\( \Rightarrow \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)\( \Leftrightarrow \overrightarrow {AM} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
Do đó \(\overrightarrow {AG} = \dfrac{2}{3}.\dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\)
Đáp án cần chọn là: b
Toán Lớp 12
