Câu hỏi
Nhận biết
Tam giác $ABC$ có$BC = 2a$, đường cao \(AD = a\sqrt 2 \). Trên đường thẳng vuông góc với $\left( {ABC} \right)$ tại $A$, lấy điểm $S$ sao cho \(SA = a\sqrt 2 \). Gọi $E,F$ lần lượt là trung điểm của $SB$ và$SC$. Diện tích tam giác $AEF$ bằng?
Đáp án đúng: c
Phương pháp giải
Tính độ dài các đoạn thẳng \(EF,AH\), từ đó suy ra diện tích tam giác.
Lời giải của Tự Học 365
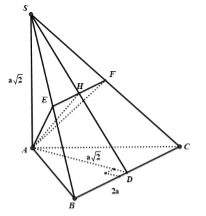
Do\(AD \bot BC,SA \bot BC \Rightarrow BC \bot \left( {SAD} \right)\)\( \Rightarrow BC \bot AH \Rightarrow EF \bot AH\)
\( \Rightarrow {S_{\Delta AEF}} = \dfrac{1}{2}EF.AH\)
Mà \(EF = \dfrac{1}{2}BC = a\). Do \(H\) là trung điểm \(SD \Rightarrow AH = \dfrac{1}{2}SD = a\) \( \Rightarrow {S_{\Delta AEF}} = \dfrac{1}{2}{a^2}\)
Đáp án cần chọn là: c
Toán Lớp 12
