Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều, \(SA \bot \left( {ABC} \right)\). Gọi $\left( P \right)$ là mặt phẳng qua $B$ và vuông góc với $SC$. Thiết diện của $\left( P \right)$ và hình chóp $S.ABC$ là:
Phương pháp giải
Sử dụng tính chất đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng.
Áp dụng: Gọi \(I\) là trung điểm của \(AC\), dựng thiết diện và nhận xét hình dạng của thiết diện.
Lời giải của Tự Học 365
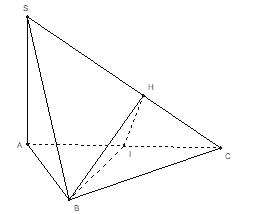
Gọi \(I\) là trung điểm của \(AC\), kẻ \(IH \bot SC\).
Ta có \(BI \bot AC,\,BI \bot SA \Rightarrow BI \bot SC\).
Do đó \(SC \bot \left( {BIH} \right)\) hay thiết diện là tam giác \(BIH\).
Mà \(BI \bot \left( {SAC} \right)\) nên \(BI \bot IH\) hay thiết diện là tam giác vuông.
Đáp án cần chọn là: d
Toán Lớp 12
