Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), cạnh bên \(SA \bot \left( {ABC} \right).\) Mặt phẳng \(\left( P \right)\) đi qua trung điểm \(M\) của \(AB\) và vuông góc với $SB$ cắt \(AC,SC,SB\) lần lượt tại \(N,P,Q.\) Tứ giác \(MNPQ\) là hình gì ?
Phương pháp giải
- Nhận xét \(BC//\left( P \right)\) rồi dựng thiết diện theo nhận xét trên.
- Nhận xét hình dạng của thiết diện dựa vào các kiến thức đã biết.
Lời giải của Tự Học 365
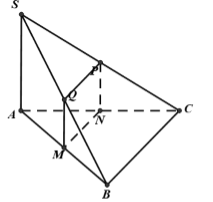
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot SB.\)
Vậy \(\left\{ \begin{array}{l}BC \bot SB\\\left( P \right) \bot SB\end{array} \right. \Rightarrow \left( P \right)//BC\left( 1 \right).\)
Mà \(\left( P \right) \cap \left( {ABC} \right) = MN\left( 2 \right).\)
Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow MN//BC\)
Tương tự ta có \(PQ//BC;PN//SA\)
Mà \(SA \bot BC \Rightarrow PN \bot NM.\)
Vậy thiết diện là hình thang \(MNPQ\) vuông tại \(N.\)
Đáp án cần chọn là: a
Toán Lớp 12
