Lời giải của Tự Học 365

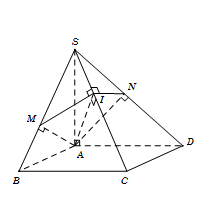
Trong tam giác $SAC, $ kẻ $AI \bot SC$ $\left( {\,I \in SC} \right)$

Trong $mp(SBC),$ kẻ ${d_1}$ đi qua $I$ vuông góc với $SC$ cắt $SB $ tại $M.$

Trong $mp(SCD),$ kẻ ${d_2}$ đi qua $I$ vuông góc với $SC$ cắt $SD$ tại $N.$

Khi đó thiết diện của hình chóp cắt bởi mp $\left( \alpha  \right)$ là tứ giác $AMIN.$

Ta có $SC \bot \left( \alpha  \right) \Rightarrow SC \bot AM$.   (1)

Lại có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM$.   (2)

Từ (1) và (2), suy ra $AM \bot \left( {SBC} \right) \Rightarrow AM \bot MI$. Chứng minh tương tự, ta được $AN \bot NI$.

Do đó ${S_{AMIN}} = {S_{\Delta AMI}} + {S_{\Delta ANI}} $ $= \dfrac{1}{2}AM.MI + \dfrac{1}{2}AN.NI$.

Vì $AM, AI, AN $ là các đường cao của các tam giác vuông $SAB, SAC, SAD $ nên

$AM = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{2a}}{{\sqrt 5 }}$;   $AI = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = a\sqrt 2 $;   $AN = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{2a\sqrt {21} }}{7}$

Suy ra $MI = \sqrt {A{I^2} - A{M^2}}  = \dfrac{{a\sqrt {30} }}{5}$  và  $NI = \sqrt {A{I^2} - A{N^2}}  = \dfrac{{a\sqrt {14} }}{7}$

Vậy ${S_{AMIN}} = \dfrac{1}{2}\left( {\dfrac{{2a}}{{\sqrt 5 }}.\dfrac{{a\sqrt {30} }}{5} + \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{a\sqrt {14} }}{7}} \right) = \dfrac{{12{a^2}\sqrt 6 }}{{35}}$

Đáp án cần chọn là: b