Cho tam giác cân $ABC,$ $AB = AC = a\sqrt 5 $ $BC = 4a.$ Trên nửa đường thẳng vuông góc với mặt phẳng chứa tam giác $ABC$ tại $A$ lấy một điểm $D$ sao cho $AD = a\sqrt 3 .$ Người ta cắt hình chóp bằng một mặt phẳng $\left( P \right)$ vuông góc với đường cao $AH$ của tam giác $ABC.$ Thiết diện là hình gì ?
Phương pháp giải
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng
Lời giải của Tự Học 365
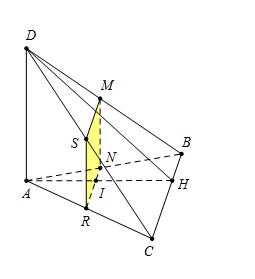
Ta có $AH$ vuông góc với $BC$ và $AD.$
Vậy $(P)$ là mặt phẳng song song với $BC$ và $AD.$
Lại có $BC // (P)$ nên $(P)$ cắt hai mặt phẳng $(ABC)$ và $(DBC)$ theo hai giao tuyến $NR$ và $MS$ với $NR // MS // BC.$
Mà $AD // (P)$ nên $\left( P \right)$ cắt hai mặt phẳng $(ACD)$ và $(BAD)$ theo hai giao tuyến $RS$ và $NM$ với $RS // MN // AD.$
Mặt khác $NM // AD$ và $AD \bot NR$\( \Rightarrow MN \bot NR\) suy ra $MNRS$ là hình chữ nhật.
Đáp án cần chọn là: c
Toán Lớp 12
