Lời giải của Tự Học 365

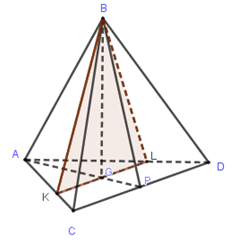
Gọi \(G\) là trọng tâm tam giác \(ACD\) thì \(BG \bot \left( {ACD} \right)\) (tính chất tứ diện đều)

Kẻ \(KL\) đi qua trọng tâm \(G\) của \(\Delta ACD\) và song song với \(CD\) \( \Rightarrow AP \bot KL\) \( \Rightarrow \left( P \right)\) chính là mặt phẳng \(\left( {BKL} \right)\) \( \Rightarrow \left( {ACD} \right) \cap \left( {BKL} \right) = KL = \dfrac{2}{3}CD = 8\)

Đáp án cần chọn là: c