Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a.$ Cạnh bên $SA$ vuông góc với $mp\,\,\left( {ABCD} \right).$ Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SB.$ Mặt phẳng $\left( \alpha \right)$ cắt hình chóp theo thiết diện là hình gì ?
Phương pháp giải
Sử dụng lý thuyết của đường thẳng vuông góc với mặt phẳng và bài toán tìm giao tuyến của hai mặt phẳng
Lời giải của Tự Học 365
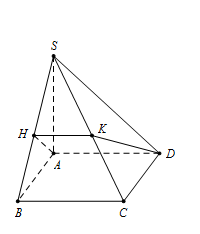
Ta có $AD$ vuông góc với $SA$ và $ AB$ $ \Rightarrow AD \bot mp\,\,\left( {SAB} \right) \Rightarrow AD \bot SB.$
Vẽ đường cao $AH$ trong tam giác $SAB$
Lại có $AD$ và $AH$ qua $A$ và vuông góc với $SB.$
Vậy mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng $(AHD).$
Mặt khác $AD // mp(SBC) $ mà $AD \subset mp\,\,\left( {AHD} \right)$
Vậy mặt phẳng $(SBC)$ cắt mặt phẳng $(AHD) $ theo giao tuyến $HK // AD.$
Do đó mặt cắt là hình thang $ADKH $ mà $AD \bot mp\,\,\left( {SAB} \right)$$ \Rightarrow \,AD \bot AH.$
Vậy $ADKH $ là hình thang vuông.
Đáp án cần chọn là: b
Toán Lớp 12
