Lời giải của Tự Học 365

Phương trình có hai nghiệm $\Leftrightarrow  \Delta ' = {\left( {m + 1} \right)^2} - \left( {{m^2} + 2} \right) = 2m + 1 \ge 0$ $\Leftrightarrow m \ge \dfrac{1}{2}$

$B = \sqrt {2\left( {x_1^2 + x_2^2} \right) + 16}  - 3{x_1}{x_2} = \sqrt {2{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2} + 16}  - 3{x_1}{x_2}$

$= \sqrt {2{{\left( {2m + 2} \right)}^2} - 4\left( {{m^2} + 2} \right) + 16}  - 3\left( {{m^2} + 2} \right) = \sqrt {4{m^2} + 16m + 16}  - 3\left( {{m^2} + 2} \right)$

$= 2m + 4 - 3\left( {{m^2} + 2} \right) =  - 3{m^2} + 2m - 2$

Xét hàm số $y =  - 3{m^2} + 2m - 2$  với $m \ge \dfrac{1}{2}$

Bảng biến thiên

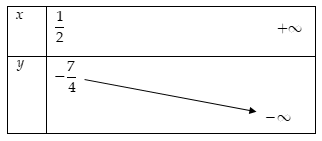
Suy ra giá trị $\mathop {\max y}\limits_{m \ge \dfrac{1}{2}}  =  - \dfrac{7}{4}$ khi $m = \dfrac{1}{2}$

Vậy giá trị lớn nhất của biểu thức $B$ là $- \dfrac{7}{4}$ khi $m = \dfrac{1}{2}$.

Đáp án cần chọn là: b