Câu hỏi
Vận dụng cao
Cho hai điểm \(A,{\rm{ }}B\) nằm ngoài \(\left( {O,R} \right)\). Điểm \(M\) di động trên \(\left( O \right).\) Dựng hình bình hành \(MABN.\) Qũy tích điểm \(N\) là
Đáp án đúng: b
Phương pháp giải
Sử dụng tính chất của phép tịnh tiến biến đường tròn thành đường tròn và xác định ảnh của \(\left( {O;R} \right)\).
Lời giải của Tự Học 365
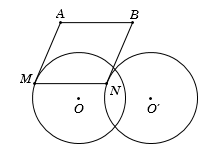
Do \(MABN\) là hình bình hành nên ta có \(\overrightarrow {MN} = \overrightarrow {AB} \). Đẳng thức này chứng tỏ phép tịnh tiến theo vectơ \(\overrightarrow {AB} \) biến điểm \(M\) thành điểm \(N\).
Mà \(M\) thuộc \(\left( {O,R} \right)\), suy ra \(N\) thuộc đường tròn \(\left( {O'} \right)\) là ảnh của \(\left( O \right)\) qua phép tịnh tiến ${T_{\overrightarrow {AB} }}.$
Đáp án cần chọn là: b
Toán Lớp 12
