Câu hỏi
Thông hiểu
Cho bốn đường thẳng \(a,{\rm{ }}b,{\rm{ }}a',{\rm{ }}b'\) trong đó $a\parallel a'$, \(b\parallel b'\) và \(a\) cắt \(b\). Có bao nhiêu phép tịnh tiến biến \(a\) thành \(a'\) và \(b\) thành \(b'\)?
Đáp án đúng: b
Phương pháp giải
Chỉ ra tất cả các phép tịnh tiến thỏa mãn bài toán và kết luận.
Lời giải của Tự Học 365
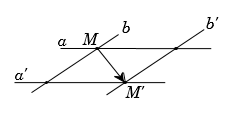
Giả sử \(a\) cắt \(b\) tại \(M;\) \(a'\) cắt \(b'\) tại \(M'.\)
Khi đó vectơ \(\overrightarrow {MM'} \) là vectơ tịnh tiến thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: b
Toán Lớp 12
