Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} $ là tập nào sau đây?
Phương pháp giải
- Biến đổi $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $.
- Sử dụng tính chất: Phép tịnh tiến biến đường tròn thành đường tròn bằng nó.
Lời giải của Tự Học 365
Từ giả thiết ta có:
$\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {MB} - \overrightarrow {MA} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $
Như thế phép tịnh tiến theo vectơ $\overrightarrow u = \overrightarrow {AB} $ biến điểm $M$ thành điểm $N$.
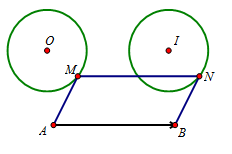
Vậy khi $M$ thay đổi trên đường tròn $\left( {O;R} \right)$ thì quỹ tích của $N$ là đường tròn $\left( {I;R} \right)$ với $\overrightarrow {OI} = \overrightarrow {AB} $.
Đáp án cần chọn là: d
Toán Lớp 12
