Cho \(\Delta ABC\) có đường cao \(AH,H\) nằm giữa \(BC.\) Biết \(AH = 4,HB = 2,HC = 8.\) Phép đồng dạng \(F\) biến \(\Delta HBA\) thành \(\Delta HAC\). \(F\) được hình thành bởi hai phép biến hình nào?
Phương pháp giải
Sử dụng tính chất: Phép đồng dạng là hợp thành của một phép vị tự và phép biến hình.
Lần lượt quan sát các đáp án và kiểm tra.
Lời giải của Tự Học 365
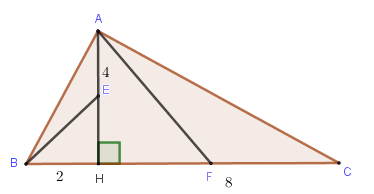
Ta có:
$\begin{array}{l}{Q_{\left( {H, - {{90}^0}} \right)}}\left( B \right) = E;{V_{\left( {H;2} \right)}}\left( E \right) = A\\{Q_{\left( {H, - {{90}^0}} \right)}}\left( A \right) = F;{V_{\left( {H;2} \right)}}\left( F \right) = C\end{array}$
Do đó, nếu ta thực hiện liên tiếp hai phép biến hình là phép quay tâm \(H\) góc quay \( - {90^0}\) và phép vị tự tâm \(H\) tỉ số \(k = 2\) ta sẽ được phép đồng dạng tỉ số \(k = 2\) biến tam giác \(\Delta HBA\) thành tam giác \(\Delta HAC\).
Đáp án cần chọn là: c
Toán Lớp 12
