Lời giải của Tự Học 365

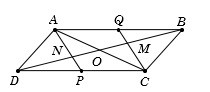
Từ giả thiết suy ra \(DN = \dfrac{2}{3}DO\), mà \(O\) là trung điểm \(AC\)\( \Rightarrow \) \(N\) là trọng tâm \(\Delta ACD\).

Mà \(AN\) cắt $CD$ tại \(P\) \( \Rightarrow \) \(P\) là trung điểm $CD$.

Tương tự, ta có: \(Q\) là trung điểm $AB$.

Do \(AQ\parallel PC\) và \(AQ = PC\) \( \Rightarrow \) \(AQCP\) là hình bình hành \( \Rightarrow \) $O$ là trung điểm của \(PQ\) \( \Rightarrow \) $P$ và $Q$ đối xứng qua $O$.

Do \(MO = NO = \dfrac{1}{6}BD\) \( \Rightarrow \) $O$ là trung điểm \(MN\) \( \Rightarrow \) $M$ và $N$ đối xứng qua $O$.

Chứng minh tương tự \( \Rightarrow \) $M$ là trọng tâm tam giác $ABC.$

Tam giác \(ABC\) không phải là tam giác đều nên không đủ kết luận \(M\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

Đáp án cần chọn là: d