Câu hỏi
Vận dụng
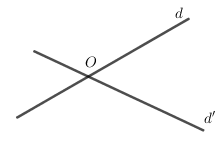
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó
Đáp án đúng: b
Phương pháp giải
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.
Lời giải của Tự Học 365
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.
Gọi $O$ là tâm đối xứng sao cho qua phép đối xứng tâm $O$ biến mỗi đường thẳng $d$ và $d'$ thành chính nó.
\( \Rightarrow \left\{ \begin{array}{l}O \in d\\O \in d'\end{array} \right. \Rightarrow O = d \cap d'\) và $O$ là duy nhất.
Đáp án cần chọn là: b
Toán Lớp 12
