Lời giải của Tự Học 365

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số $y = {x^2} - 2x + \left| {2x - 3} \right|$ và đường thẳng $y = m$ có tính chất song song với trục hoành.

Đồ thị hàm số $y = {x^2} - 2x + \left| {2x - 3} \right| = \left\{ \begin{array}{l}{x^2} - 2x + 2x - 3 = {x^2} - 3\,\,\left( {{P_1}} \right)\,\,khi\,\,x \ge \dfrac{3}{2}\\{x^2} - 2x - 2x + 3 = {x^2} - 4x + 3\,\,\left( {{P_2}} \right)\,\,khi\,x < \dfrac{3}{2}\end{array} \right.$ được vẽ như sau:

+ Vẽ lần lượt hai đồ thị hàm số trên cùng một hệ trục tọa độ

+ Xóa đi nhánh bên trái điểm \(x = \dfrac{3}{2}\) của đồ thị hàm số \(y = {x^2} - 3\)

+ Xóa đi nhánh bên phải điểm \(x = \dfrac{3}{2}\) của đồ thị hàm số \(y = {x^2} - 4x + 3\)

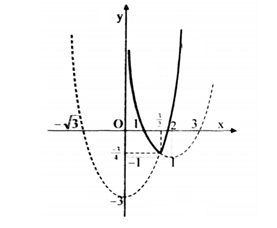
Tọa độ giao điểm của đồ thị hàm số \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) là : \(\left( {\dfrac{3}{2}; - \dfrac{3}{4}} \right)\)

Dựa trên đồ thị ta thấy phương trình đã cho có nghiệm duy nhất khi và chỉ khi $m =  - \dfrac{3}{4}$.

Đáp án cần chọn là: c