Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ như hình vẽ bên
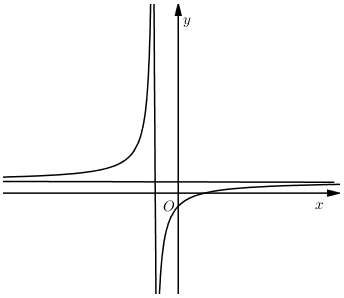
Chọn khẳng định đúng
Phương pháp giải
- Tìm các tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
- Tìm các giao điểm của đồ thị hàm số với hai trục tọa độ.
- Xét tính đơn điệu của hàm số.
- Kết hợp các kết quả trên ta được điều kiện của $a,b,c,d$.
Lời giải của Tự Học 365
Đồ thị hàm số $y = \dfrac{{ax + b}}{{cx + d}}$ có:
- TCĐ $x = - \dfrac{d}{c} < 0 \Rightarrow cd > 0$
- TCN $y = \dfrac{a}{c} > 0 \Rightarrow ac > 0$
$ \Rightarrow ac.cd > 0 \Rightarrow ad > 0 \Rightarrow $Loại A, B.
- $y' = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}} > 0 \Rightarrow ad > bc$
- Cắt $Oy:x = 0 \Rightarrow y = \dfrac{b}{d} < 0 \Rightarrow bd < 0$
- Cắt $Ox:y = 0 \Rightarrow x = - \dfrac{b}{a} > 0 \Rightarrow ab < 0$
Vì $ac > 0;ab < 0$ nên $ac.ab < 0 \Rightarrow bc < 0 \Rightarrow $ Loại D
Đáp án cần chọn là: c
Toán Lớp 12
