Câu hỏi
Vận dụng
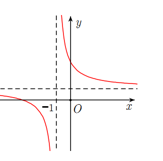
Cho hàm số \(y = \dfrac{{ax + b}}{{x + 1}}\) có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:
Đáp án đúng: d
Phương pháp giải
Dựa vào TCN của đồ thị hàm số và giao điểm của đồ thị hàm số với trục hoành.
Lời giải của Tự Học 365
Đồ thị hàm số có đường tiệm cận ngang \(y = a\). Theo hình vẽ, ta có: \(a > 0.\)
Đồ thị hàm số cắt trục hoành tại điểm \(A\left( { - \dfrac{b}{a};0} \right)\)
Theo hình vẽ, ta có: \( - \dfrac{b}{a} < - 1 \Leftrightarrow \dfrac{b}{a} > 1 \Rightarrow \dfrac{{b - a}}{a} > 0\).
Mà \(a > 0 \Rightarrow b - a > 0 \Leftrightarrow b > a\)
Vậy \(b > a > 0\).
Đáp án cần chọn là: d
Toán Lớp 12
