Câu hỏi
Vận dụng
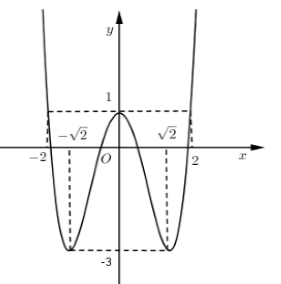
Đồ thị hàm số bên là đồ thị của hàm số \(y = {x^4} - 4{x^2} + 1\left( C \right).\) Tìm m để phương trình \({x^4} - 4{x^2} + 1 - m = 0\) có \(2\) nghiệm phân biệt
Đáp án đúng: c
Phương pháp giải
Quan sát đồ thị hàm số và nhận xét: Số nghiệm của phương trình là số giao điểm của đường thẳng với đồ thị hàm số.
Lời giải của Tự Học 365
\({x^4} - 4{x^2} + 1 - m = 0 \Leftrightarrow {x^4} - 4{x^2} + 1 = m\)
Số nghiệm của phương trình \({x^4} - 4{x^2} + 1 - m = 0\) là số giao diểm của đồ thị hàm số \(y = {x^4} - 4{x^2} + 1 - m\) và đường thẳng \(y = m\).
Vậy để phương trình \({x^4} - 4{x^2} + 1 - m = 0\) có \(2\) nghiệm phân biệt \( \Leftrightarrow m > 1\) hoặc \(m = - 3\)
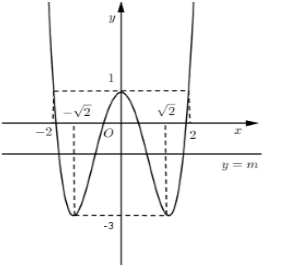
Đáp án cần chọn là: c
Toán Lớp 12
