Câu hỏi
Vận dụng
Cho hàm số $y = a{x^3} + b{x^2} + cx + d\,\left( {a e 0} \right)$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu của $a,b,c,d$ là đúng nhất?
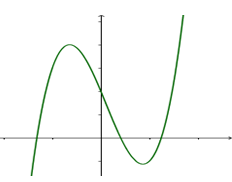
Đáp án đúng: d
Phương pháp giải
Chú ý dạng của đồ thị hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d\,\left( {a e 0} \right)$
Lời giải của Tự Học 365
$\mathop {\lim }\limits_{x \to - \infty } x = - \infty $ nên $a > 0$
Dựa vào đồ thị hàm số ta có $y' = 3a{x^2} + 2bx + c = 0$ có hai nghiệm phân biệt trái dấu
$ \Rightarrow ac < 0$ mà $a > 0$ nên suy ra $c < 0$ suy ra loại B, C.
Mặt khác thấy đồ thị cắt trục $Oy$ tại điểm có tung độ dương $ \Rightarrow d > 0$
Đáp án cần chọn là: d
Toán Lớp 12
