Câu hỏi
Vận dụng
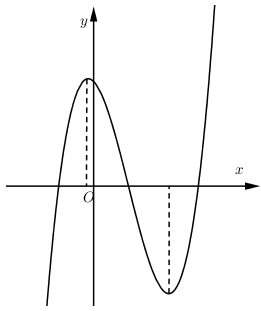
Hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
Đáp án đúng: d
Phương pháp giải
Quan sát đồ thị và nhận xét dạng đồ thị, điểm đi qua, điểm cực đại, cực tiểu,…
Lời giải của Tự Học 365
Nhận xét: Hàm số bậc 3 có $2$ cực trị và hệ số $a > 0$
Khi $x = 0$ Þ $y = d > 0$
$y' = 3a{x^2} + 2bx + c$ có $2$ nghiệm phân biệt trái dấu Þ $3ac < 0 $Þ $c < 0$ (Vì $a > 0$)
$\dfrac{{{x_1} + {x_2}}}{2} > 0 \Leftrightarrow \dfrac{{\dfrac{{ - 2b}}{{3a}}}}{2} > 0 \Leftrightarrow \dfrac{{ - b}}{{3a}} > 0 \Rightarrow - b > 0\,(Do\,a > 0) \Rightarrow b < 0$
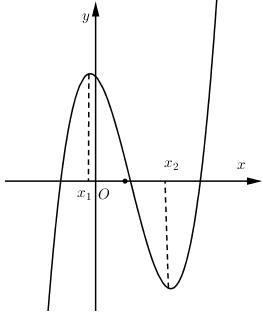
Vậy khẳng định đúng là: $a > 0, b < 0, c < 0, d > 0$
Đáp án cần chọn là: d
Toán Lớp 12
