Câu hỏi
Thông hiểu
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông cân đỉnh $A,AB = AC = a,AA' = a\sqrt 2 $. Diện tích mặt cầu ngoại tiếp tứ diện $A'BB'C$ là:
Đáp án đúng: b
Phương pháp giải
- Xác định tâm mặt cầu ngoại tiếp từ diện $A'BB'C$
- Tính bán kính mặt cầu ngoại tiếp tứ diện $A'BB'C$
- Diện tích mặt cầu: $S = 4\pi {R^2}$
Lời giải của Tự Học 365
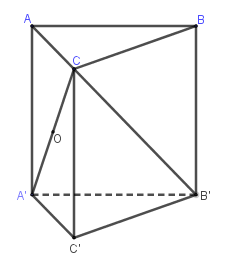
Ta có: $BC = B'B = a\sqrt 2 ,B'C = 2a;A'C = a\sqrt 3 $
Do $A'B' \bot \left( {B'BC} \right)$ và $\Delta B'BC$ vuông cân tại $B$
$ \Rightarrow $ Tâm $O$ của mặt cầu ngoại tiếp tứ diện $A'BB'C$
là trung điểm của $A'C$
$ \Rightarrow R = \dfrac{{a\sqrt 3 }}{2}$
$ \Rightarrow S = 4\pi .{R^2} = 4\pi .\dfrac{{3{a^2}}}{4} = 3\pi {a^2}$
Đáp án cần chọn là: b
Toán Lớp 12
