Lời giải của Tự Học 365

Do $D$ đối xứng với $C$ qua $B$ nên có $BC = DC = AC$ suy ra tam giác $ABD$ là tam giác vuông tại $A$.

Kẻ đường thẳng $d$ qua $C$ vuông góc với đáy, đường thẳng này là trục đường tròn ngoại tiếp tam giác đáy $ABD$ .

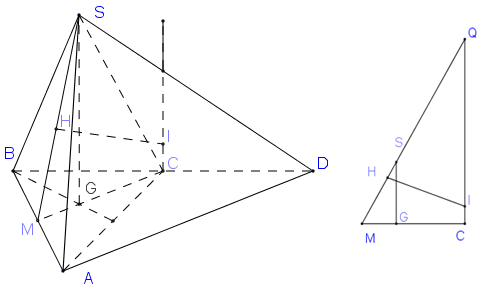
Tam giác $SAB$ cân tại $S$ , gọi $M$ là trung điểm $AB,H$ là tâm đường tròn ngoại tiếp tam giác $SAB$

 \( \Rightarrow H \in SM;SM = \sqrt {S{A^2} - A{M^2}}  = \dfrac{{a\sqrt {13} }}{{2\sqrt 3 }}\)

\(SH = \dfrac{{AB.SA.SB}}{{4.{S_{SAB}}}} = \dfrac{{{{\left( {\dfrac{{2a}}{{\sqrt 3 }}} \right)}^2}.a}}{{4.\dfrac{1}{2}.a.AM}} = \dfrac{{4a}}{{\sqrt {39} }}\)

Trong $\left( {SAC} \right)$  dựng\(HI \bot SM\left( {I \in d} \right)(1)\).

Mà \(\left\{ \begin{array}{l}AB \bot SM\\AB \bot MC\end{array} \right. \Rightarrow AB \bot \left( {SMC} \right) \Rightarrow AB \bot HI(2)\)

Từ (1), (2) suy ra \(HI \bot \left( {SAB} \right)\) , suy ra $I$ là tâm đường tròn ngoại tiếp hình chóp $S.ABD$

Gọi \(Q = MS \cap CI\), xét tam giác $SCM$ có

\(\dfrac{{SM}}{{QM}} = \dfrac{{MG}}{{MC}} = \dfrac{1}{3}\) \( \Rightarrow QM = 3SM = 3.\dfrac{{a\sqrt {13} }}{{2\sqrt 3 }} = \dfrac{{a\sqrt {39} }}{2}\)

\( \Rightarrow QH = QM - MS + HS\) \( = \dfrac{{a\sqrt {39} }}{2} - \dfrac{{a\sqrt {13} }}{{2\sqrt 3 }} + \dfrac{{4a}}{{\sqrt {39} }} = \dfrac{{17a}}{{\sqrt {39} }}\)

\(QC = \sqrt {Q{M^2} - M{C^2}}  = 3a\)

Xét: \(\Delta QHI \sim \Delta QCM \Rightarrow \dfrac{{HI}}{{CM}} = \dfrac{{HQ}}{{QC}}\) \( \Rightarrow HI = \dfrac{{HQ.CM}}{{QC}} = \dfrac{{17a}}{{6\sqrt {13} }}\)

\( \Rightarrow R = SI = \sqrt {H{I^2} + H{S^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt {17} }}{{6\sqrt {13} }}} \right)}^2} + {{\left( {\dfrac{{4a}}{{\sqrt {39} }}} \right)}^2}}  = \dfrac{{a\sqrt {37} }}{6}\)

Đáp án cần chọn là: c