Câu hỏi
Thông hiểu
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên \(b\). Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:
Đáp án đúng: a
Phương pháp giải
Sử dụng công thức tính bán kính mặt cầu ngoại tiếp hình chóp đều: \(R = \dfrac{{{b^2}}}{{2h}}\) với \(b\) là độ dài cạnh bên,
\(h\) là chiều cao hình chóp.
Lời giải của Tự Học 365
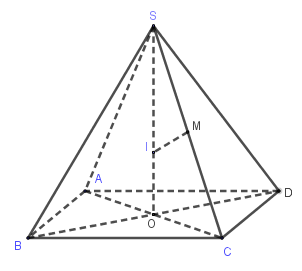
Ta có: \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = a\sqrt 2 \Rightarrow OA = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}\)
Tam giác \(SOC\) vuông tại \(O\) nên \(S{C^2} = S{O^2} + O{C^2} \Rightarrow h = SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{2}} \)
Vậy \(R = \dfrac{{{b^2}}}{{2h}} = \dfrac{{{b^2}}}{{2\sqrt {{b^2} - \dfrac{{{a^2}}}{2}} }}\)
Đáp án cần chọn là: a
Toán Lớp 12
