Câu hỏi
Thông hiểu
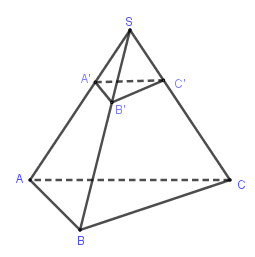
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
Đáp án đúng: c
Phương pháp giải
Sử dụng định nghĩa phép vị tự --- Xem chi tiếtLời giải của Tự Học 365
Ta có: \(A'A = 2SA',B'B = 2SB',C'C = 2SC' \)
$\Rightarrow \overrightarrow {SA'} = \dfrac{1}{3}\overrightarrow {SA} ,\overrightarrow {SB'} = \dfrac{1}{3}\overrightarrow {SB} ,\overrightarrow {SC'} = \dfrac{1}{3}\overrightarrow {SC} $
Do đó phép vị tự tâm \(S\) tỉ số \(k = \dfrac{1}{3}\) biến các điểm \(A,B,C\) thành \(A',B',C'\).
Đáp án cần chọn là: c
Toán Lớp 12
