Lời giải của Tự Học 365

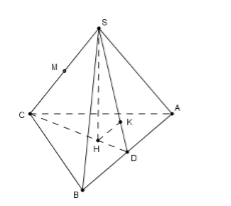
Gọi \(D\) là trung điểm của \(AB,\,\,H\) là trọng tâm tam giác \(ABC\).

Khi đó \(SH \bot \left( {ABC} \right)\) do \(S.ABC\) là hình chóp đều.

Kẻ \(HK \bot SD\) tại \(K.\)

Ta có \(\left\{ \begin{array}{l}AB \bot CD\,\,\left( {do\,\,\Delta ABC\,\,deu} \right)\\AB \bot SH\left( {do\,SH \bot \left( {ABC} \right)} \right)\end{array} \right. \Leftrightarrow AB \bot \left( {SDC} \right) \Rightarrow AB \bot HK\)

Mà \(HK \bot SD \Rightarrow HK \bot \left( {SAB} \right)\) tại \(K \Rightarrow d\left( {H,\left( {SAB} \right)} \right) = HK\)

+) Vì tam giác \(ABC\) đều cạnh \(3a\) nên

\(CD = \dfrac{{\sqrt 3 }}{2}.3a = \dfrac{{3\sqrt 3 a}}{2} \Rightarrow HD = \dfrac{1}{3}CD = \dfrac{{\sqrt 3 }}{2}a;\,\,HC = \dfrac{2}{3}CD = \sqrt 3 a\)

Vì \(S.ABC\) là chóp đều nên \(SC = SA = 2a\) .

Xét tam giác \(SHC\) vuông tại \(C,\) theo định lý Pytago ta có \(SH = \sqrt {S{C^2} - H{C^2}}  = \sqrt {4{a^2} - 3{a^2}}  = a\).

+) Xét tam giác \(SHD\) vuông tại \(H,\) ta có \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{\dfrac{3}{4}{a^2}}} = \dfrac{7}{{3{a^2}}} \Rightarrow HK = \dfrac{{a\sqrt {21} }}{7}\)

+) Ta có \(\dfrac{{d\left( {C,\left( {SAB} \right)} \right)}}{{d\left( {H,\left( {SAB} \right)} \right)}} = \dfrac{{CD}}{{HD}} = 3 \Leftrightarrow d\left( {C;\left( {SAB} \right)} \right) = 3.d\left( {H;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{7}\).

Lại có \(\dfrac{{d\left( {M,\left( {SAB} \right)} \right)}}{{d\left( {C,\left( {SAB} \right)} \right)}} = \dfrac{{MA}}{{CA}} = \dfrac{1}{2} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \dfrac{1}{2}.d\left( {C;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{{14}}\)

Đáp án cần chọn là: d