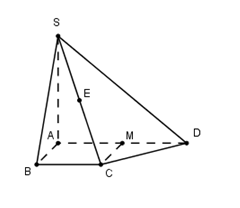
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\), $AD = 2BC,$ $AB = BC = a\sqrt 3 $. Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(E\) là trung điểm của cạnh \(SC\). Tính khoảng cách \(d\) từ điểm \(E\) đến mặt phẳng \(\left( {SAD} \right)\).
Phương pháp giải
Sử dụng phương pháp kẻ chân đường cao từ điểm đến mặt phẳng (lý thuyết đường thẳng vuông góc với mặt phẳng) để xác định khoảng cách từ một điểm đến mặt phẳng
Lời giải của Tự Học 365
Ta có
\(\begin{array}{l}EC \cap \left( {SAD} \right) = S \Rightarrow \dfrac{{d\left( {E;\left( {SAD} \right)} \right)}}{{d\left( {C;\left( {SAD} \right)} \right)}} = \dfrac{{ES}}{{CS}} = \dfrac{1}{2}\\ \Rightarrow d\left( {E;\left( {SAD} \right)} \right) = \dfrac{1}{2}d\left( {C;\left( {SAD} \right)} \right)\end{array}\).
Gọi M là trung điểm AM, suy ra ABCM là hình vuông \( \Rightarrow CM \bot AD\).
Do \(\left\{ \begin{array}{l}CM \bot AD\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAD} \right) \Rightarrow d\left( {C;\left( {SAD} \right)} \right) = CM = AB = a\sqrt 3 \)
Vậy \(d\left( {E;\left( {SAD} \right)} \right) = \dfrac{1}{2}CM = \dfrac{{a\sqrt 3 }}{2}.\)
Đáp án cần chọn là: c
Toán Lớp 12
