Câu hỏi
Thông hiểu
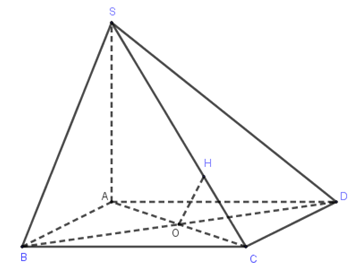
Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, $SA = 2a$, $ABCD$ là hình vuông cạnh bằng $a$. Gọi $O$ là tâm của $ABCD$, tính khoảng cách từ $O$ đến $SC$.
Đáp án đúng: a
Phương pháp giải
Kẻ \(OH \bot SC\) và tính độ dài \(OH\) dựa vào tam giác đồng dạng và một số hệ thức giữa cạnh và đường coa trong tam giác vuông.
Lời giải của Tự Học 365
Kẻ $OH \bot SC$, khi đó $d\left( {O,SC} \right) = OH$. Ta có: $\Delta SAC \sim \Delta OHC(g-g)$ nên $\dfrac{{OH}}{{SA}} = \dfrac{{OC}}{{SC}} \Rightarrow OH = \dfrac{{OC}}{{SC}}.SA$.
Mà: $OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2},SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 6 $
Vậy $OH = \dfrac{{OC}}{{SC}}.SA = \dfrac{a}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}$
Đáp án cần chọn là: a
Toán Lớp 12
