Câu hỏi
Nhận biết
Cho hình chóp $A.BCD$có cạnh $AC \bot \left( {BCD} \right)$và $BCD$ là tam giác đều cạnh bằng $a$. Biết $AC = a\sqrt 2 $, khoảng cách từ $A$ đến đường thẳng $BD$ bằng:
Đáp án đúng: d
Phương pháp giải
Gọi \(M\) là trung điểm của \(BD\) và chứng minh khoảng cách cần tìm là \(AM\).
Lời giải của Tự Học 365
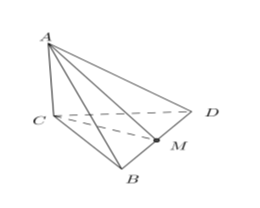
Gọi \(M\) là trung điểm của \(BD\).
Ta có: $\left\{ \begin{array}{l}AC \bot BD\\CM \bot BD\end{array} \right. \Rightarrow BD \bot AM$ (Định lý 3 đường vuông góc) $ \Rightarrow d\left( {A;BD} \right) = AM$.
$CM = \dfrac{{a\sqrt 3 }}{2}$ (vì tam giác $BCD$ đều).
Ta có: $AM = \sqrt {A{C^2} + M{C^2}} = \sqrt {2{a^2} + \dfrac{{3{a^2}}}{4}} = \dfrac{{a\sqrt {11} }}{2}$.
Đáp án cần chọn là: d
Toán Lớp 12
