Câu hỏi
Thông hiểu
Cho hình chóp \(S.ABCD\)có đáy là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm của \(CD\). Khoảng cách từ \(M\) đến \(SA\) nhận giá trị nào trong các giá trị sau?
Đáp án đúng: a
Phương pháp giải
Chứng minh khoảng cách cần tìm là \(MA\) và tính khoảng cách đó.
Lời giải của Tự Học 365
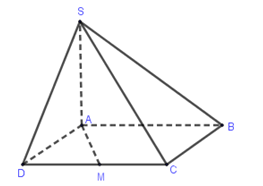
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot MA\) hay \(A\) là hình chiếu của \(M\) trên \(SA\).
Khi đó \(d\left( {M,SA} \right) = MA = \sqrt {A{D^2} + D{M^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\)
Đáp án cần chọn là: a
Toán Lớp 12
