Câu hỏi
Nhận biết
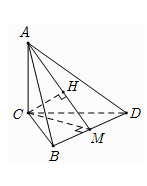
Cho hình chóp $A.BCD$ có cạnh $AC \bot \left( {BCD} \right)$ và $BCD$ là tam giác đều cạnh bằng $a.$ Biết $AC = a\sqrt 2 $ và $M$ là trung điểm của $BD.$ Khoảng cách từ $C$ đến đường thẳng $AM$ bằng
Đáp án đúng: c
Phương pháp giải
- Dựng hình chiếu \(H\) của \(C\) trên \(AM\).
- Sử dụng các hệ thức trong tam giác vuông để tính \(CH\)
Lời giải của Tự Học 365
Dựng hình chiếu $H$ của $C$ trên $AM$
Do \(\Delta BCD\) đều cạnh \(a\) nên đường cao \(MC = \dfrac{{a\sqrt 3 }}{2}\)
\(d\left( {C,AM} \right) = CH = \dfrac{{AC.MC}}{{\sqrt {A{C^2} + M{C^2}} }} = \dfrac{{a\sqrt {66} }}{{11}}\)
Đáp án cần chọn là: c
Toán Lớp 12
