Lời giải của Tự Học 365

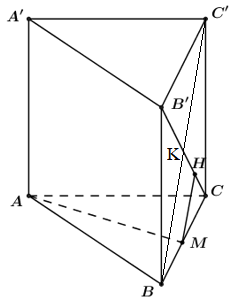
Ta có : \(\left\{ \begin{align} & AM\bot BC \\ & AM\bot BB' \\ \end{align} \right.\Rightarrow AM\bot \left( BCC'B' \right)\)

Trong \(\left( BCC'B' \right)\) kẻ \(MH//BC'\,\,\left( H\in B'C \right)\Rightarrow MH\bot B'C\)

\(MH\subset \left( BCC'B' \right)\Rightarrow AM\bot MH\)

\(\Rightarrow MH\) là đoạn vuông góc chung giữa AM và B’C \(\Rightarrow d\left( AM;B'C \right)=MH\)

Dễ thấy \(MH = \frac{1}{2}BK = \frac{1}{4}B'C = \frac{{a\sqrt 2 }}{4}\) với \(K\) là trung điểm của \(B'C\).

\(\Rightarrow d\left( AM;B'C \right)=\frac{a\sqrt{2}}{4}\)

Đáp án cần chọn là: b