Lời giải của Tự Học 365

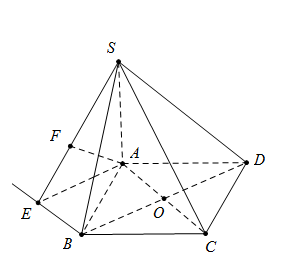
Ta có $AC = a\sqrt 2 ;\widehat {SCA} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = {45^0} \Rightarrow SA = AC = a\sqrt 2 $

Dựng $Bx||AC \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;(SBx)} \right)$

Dựng $AE \bot Bx,\;AF \bot SE\,\,\,\left( 1 \right)$ ta có:

\(\left\{ \begin{array}{l}Bx \bot AE\\Bx \bot SA\end{array} \right. \Rightarrow Bx \bot \left( {SAE} \right) \Rightarrow Bx \bot AF\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow AF \bot \left( {SBE} \right)\)  \( \Rightarrow d = d\left( {AC;\left( {SBx} \right)} \right) = d\left( {A,\left( {SBx} \right)} \right) = AF\)

Ta có $BE||AC \Rightarrow BE \bot BD$ dễ ràng suy ra $OEBO$ là hình chữ nhật suy ra $AE = OB = \dfrac{{a\sqrt 2 }}{2}.$

Vậy khoảng cách

$d\left( {SB;AC} \right) = \dfrac{{AE.SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a\sqrt 2 }}{{\sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \dfrac{{a\sqrt {10} }}{5}$.

Đáp án cần chọn là: c