Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh bằng 10. Tính khoảng cách giữa hai mặt phẳng (ADD’A’) và (BCC’B’).
Phương pháp giải
Xác định khoảng cách giữa hai mặt phẳng song song (P) và (Q).
\(d\left( \left( P \right);\left( Q \right) \right)=d\left( M;\left( Q \right) \right)=MH\) với \(M\) là điểm bất kỳ thuộc \(\left( P \right)\) và \(H\) là hình chiếu của \(M\) lên mặt phẳng \(\left( Q \right)\).
Lời giải của Tự Học 365
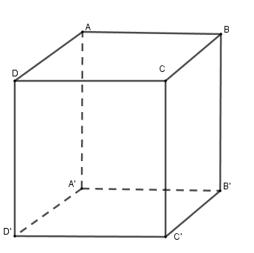
Vì \(ABCD.{A}'{B}'{C}'{D}'\) là hình lập phương nên \(\left( AD{D}'{A}' \right)\)// \(\left( BC{C}'{B}' \right)\).
Khi đó \(d\left( \left( AD{D}'{A}' \right);\left( BC{C}'{B}' \right) \right)=d\left( A;\left( BC{C}'{B}' \right) \right)\)
Mà \(AB\bot \left( BC{C}'{B}' \right)\) nên \(d\left( A;\left( BC{C}'{B}' \right) \right)=AB=10\).
Đáp án cần chọn là: c
Toán Lớp 12
