Lời giải của Tự Học 365

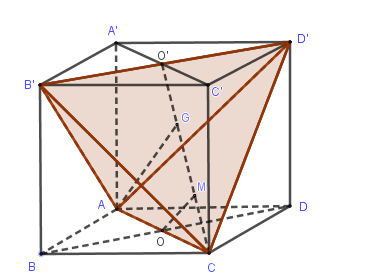
Gọi \(O,O'\) lần lượt là tâm hai đáy \(ABCD,A'B'C'D'\) .

Vì \(BD//B'D'\) nên \(BD//\left( {CB'D'} \right)\).

Do đó \(d\left( {BD,\left( {CB'D'} \right)} \right) = d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Mà \(AO \cap \left( {CB'D'} \right) = C \Rightarrow d\left( {O,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Vậy \(d\left( {BD,\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right)\)

Ta tính \(d\left( {A,\left( {CB'D'} \right)} \right)\).

Xét tứ diện \(ACB'D'\) có \(AB' = AC = AD' = B'C = B'D' = CD' = a\sqrt 2 \) nên nó là tứ diện đều cạnh \(a\sqrt 2 \).

Gọi \(G\) là trọng tâm tam giác \(CB'D'\) thì \(CG = \dfrac{2}{3}CO' = \dfrac{2}{3}.\dfrac{{a\sqrt 2 .\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{3}\)

Do đó \(d\left( {A,\left( {CB'D'} \right)} \right) = AG = \sqrt {A{C^2} - C{G^2}}  = \sqrt {2{a^2} - \dfrac{{6{a^2}}}{9}}  = \dfrac{{2a\sqrt 3 }}{3}\)

Vậy \(d\left( {BD;\left( {CB'D'} \right)} \right) = \dfrac{1}{2}d\left( {A,\left( {CB'D'} \right)} \right) = \dfrac{{a\sqrt 3 }}{3}\).

Đáp án cần chọn là: c