Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 4,{\rm{ }}AD = 3.\) Mặt phẳng \((ACD')\) tạo với mặt đáy một góc \({60^ \circ }.\) Tính khoảng cách giữa hai mặt đáy của hình hộp.
Phương pháp giải
- Xác định góc giữa hai mặt phẳng \(\left( {ACD'} \right)\) và \(\left( {ABCD} \right)\) theo dấu hiệu: góc giữa hai mặt là góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến tại một điểm.
- Khoảng cách giữa hai mặt đáy của hình hộp chữ nhật chính là độ dài cạnh bên của hình hộp.
Lời giải của Tự Học 365
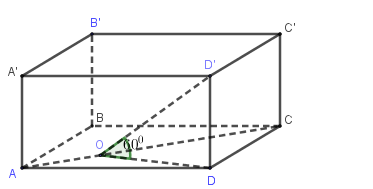
Gọi \(O\) là hình chiếu của \(D\) lên \(AC\).
Ta có \(\left\{ \begin{array}{l}\left( {ACD'} \right) \cap \left( {ABCD} \right) = AC\\AC \bot DO\\AC \bot D'O\left( {AC \bot \left( {ODD'} \right) \supset OD'} \right)\end{array} \right.\)
\( \Rightarrow \left( {\widehat {\left( {D'AC} \right),\left( {ABCD} \right)}} \right) = \widehat {D'OD} = {60^0}\)
\(AC = \sqrt {{3^2} + {4^2}} = 5\) ; \(DO = \dfrac{{AD.DC}}{{AC}} = \dfrac{{12}}{5}\)
Khoảng cách giữa hai mặt đáy là \(DD' = DO.\tan {60^0} = \dfrac{{12\sqrt 3 }}{5}\)
Đáp án cần chọn là: b
Toán Lớp 12
