Lời giải của Tự Học 365

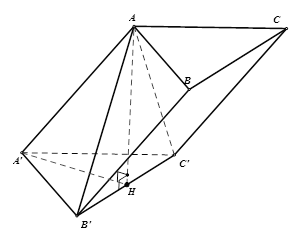
Do hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\) nên \(A'A = a\).

\(H\) là hình chiếu của \(A\) trên \(\left( {A'B'C'} \right)\) nên \(AH \bot \left( {A'B'C'} \right) \Rightarrow d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = AH = \dfrac{a}{2}\)

\(\Delta A'HA\) vuông tại \(H\) nên \(A'H = \sqrt {A'{A^2} - A{H^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Mặt khác \(\Delta A'B'C'\) đều cạnh \(a\) nên đường cao \(A'H' = \dfrac{{a\sqrt 3 }}{2}\) ($H'$ là trung điểm của $B'C'$)

Từ đó \(A'H = A'H'\) và \(H,H' \in B'C'\) nên \(H \equiv H'\).

Vậy \(H\) là trung điểm của \(B'C' \Rightarrow HB' = \dfrac{1}{2}B'C'\).

Đáp án cần chọn là: b