Cho hình chóp $O.ABC$ có đường cao $OH = \dfrac{{2a}}{{\sqrt 3 }}$. Gọi $M$ và $N$ lần lượt là trung điểm của $OA$ và $OB.$ Khoảng cách giữa đường thẳng $MN$ và $\left( {ABC} \right)$ bằng:
Phương pháp giải
- Chứng minh \(MN//\left( {ABC} \right) \Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right).\)
- Tính \(d\left( {M,\left( {ABC} \right)} \right)\) bằng phương pháp tỉ số khoảng cách.
Lời giải của Tự Học 365
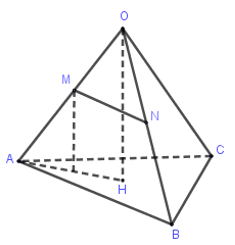
Vì $M$ và $N$ lần lượt là trung điểm của $OA$ và $OB$ nên $MN//AB \Rightarrow MN//\left( {ABC} \right)$.
Ta có: \(d\left( {MN;\left( {ABC} \right)} \right) = d\left( {M;\left( {ABC} \right)} \right) \)
Vì \(OM\) cắt \((ABC)\) tại \(A\) và \(OA=2MA\) nên \(d\left( {M;\left( {ABC} \right)} \right)= \dfrac{1}{2}OH = \dfrac{{a\sqrt 3 }}{3}\).
Đáp án cần chọn là: d
Toán Lớp 12
