Cho hình thang vuông $ABCD$ vuông ở $A$ và $D$, $AD = 2a.$ Trên đường thẳng vuông góc với $\left( {ABCD} \right)$ tại $D$ lấy điểm $S$ với $SD = a\sqrt 2 .$ Tính khỏang cách giữa đường thẳng $DC$ và $\left( {SAB} \right)$.
Phương pháp giải
Chứng minh \(CD//\left( {SAB} \right) \Rightarrow d\left( {CD,\left( {SAB} \right)} \right) = d\left( {D,\left( {SAB} \right)} \right)\)
Lời giải của Tự Học 365
Vì $DC$// $AB$ nên $DC$// $\left( {SAB} \right)$
$ \Rightarrow d\left( {DC;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right)$.
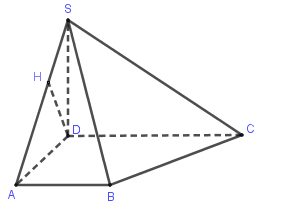
Kẻ $DH \bot SA$, do $AB \bot AD$, $AB \bot SD$ nên $AB \bot \left( {SAD} \right) \Rightarrow DH \bot AB$ suy ra $d\left( {D;\left( {SAB} \right)} \right) = DH$.
Trong tam giác vuông $SAD$ ta có:
$\dfrac{1}{{D{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}}$$ \Rightarrow DH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \dfrac{{2a}}{{\sqrt 3 }}$.
Đáp án cần chọn là: a
Toán Lớp 12
