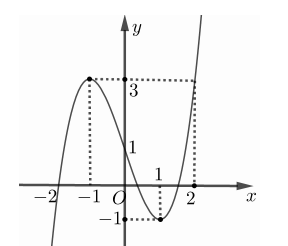
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây. Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(f\left( {3 - \sqrt {4 - {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\). Tìm tập \(S\).
Phương pháp giải
- Đặt ẩn phụ \(t = 3 - \sqrt {4 - {x^2}} \).
- Nhận xét số nghiệm của phương trình ẩn \(t\) với số nghiệm của phương trình ẩn \(x\) suy ra điều kiện tương đương phương trình ẩn \(t\).
Lời giải của Tự Học 365
Đặt \(t = 3 - \sqrt {4 - {x^2}} \) \( \Rightarrow 3 - t = \sqrt {4 - {x^2}} \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = 4 - {\left( {3 - t} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = \left( {t - 1} \right)\left( {5 - t} \right) \ge 0\end{array} \right. \Rightarrow 1 \le t \le 3\)
Nhận thấy với \(t = 1\) thì \({x^2} = 0 \Leftrightarrow x = 0\) hay với \(t = 1\) thì ta chỉ tìm được đúng một nghiệm \(x\) (loại)
Với \(1 < t \le 3\) thì \({x^2} > 0\) nên ta sẽ tìm được hai giá trị của \(x\) đối nhau.
Do đó để phương trình có hai nghiệm phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\) thì phương trình phải có hai nghiệm phân biệt đối nhau thuộc \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\) và \(x e 0\).
Dễ thấy \(x \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\backslash \left\{ 0 \right\} \Rightarrow {x^2} \in \left( {0;2} \right] \Rightarrow 4 - {x^2} \in \left[ {2;4} \right)\)
\( \Rightarrow \sqrt {4 - {x^2}} \in \left[ {\sqrt 2 ;2} \right) \Rightarrow 3 - \sqrt {4 - {x^2}} \in \left( {1;3 - \sqrt 2 } \right]\)
\( \Rightarrow t \in \left( {1;3 - \sqrt 2 } \right] \Rightarrow f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right]\) vì \(f\left( t \right)\) đồng biến trên \(\left( {1;3 - \sqrt 2 } \right]\).
Phương trình đã cho có hai nghiệm \({x_1},{x_2}\) phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\) thì phương trình \(f\left( t \right) = m\) có nghiệm duy nhất \(t \in \left( {1;3 - \sqrt 2 } \right]\)
\( \Rightarrow m = f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right] = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right]\).
Vậy \(S = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right]\).
Đáp án cần chọn là: a
Toán Lớp 12
