Lời giải của Tự Học 365

Hàm số chỉ có 1 cực trị thì $y' = 0$ có 1 nghiệm $ \Leftrightarrow ab \ge 0$, khi đó đồ thị có dạng:

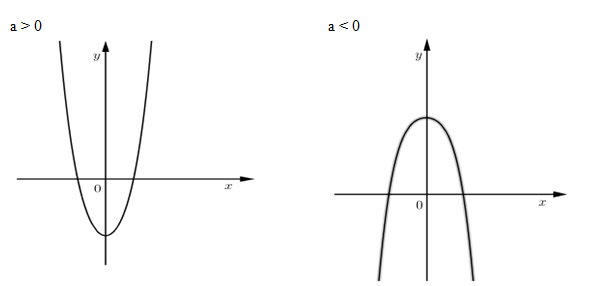
Trong hai trường hợp trên ta thấy nếu đồ thị hàm số nằm hoàn toàn phía trên trục hoành thì chỉ xảy ra trường hợp $a > 0$, do đó $b \ge 0$ và điểm cực tiểu $\left( {0;c} \right)$ cũng phải nằm phía trên trục hoành hay $c > 0$.

Đáp án cần chọn là: a